I spent 3 months over the summer on a break from work (if you’re feeling pretentious, feel free to call it a sabbatical) mostly to keep a promise I made to myself a decade ago: when I was interviewing at Google my recruiter had warned me that without a degree (which I lacked) I might succeed at interview and fall at the final hurdle. So I booked onto a MSc at Sussex, absolutely loved it, and ended it swearing I’d take a year off every ten thereon to focus on lifelong learning. Then I blinked, ten years had passed, and I found myself thinking awkwardly about how to keep both this promise and my job. I’m exceptionally fortunate to have an employer with a generous view of taking time out, so that’s what I did.

Common advice online was to start any break with a complete change of scene and habits, so I spent the first month in Tuscany, tucked away in the countryside near Figline Valdarno (between Florence and Siena) with a pile of books, some walking boots and my running shoes. I slept voraciously, read indulgently, and hiked around the local countryside until I was sick of the sight of terracotta and lush greenery. Towards the end my dad came out to visit and we continued in this vein together.

Then it was back to the Bay Area, where to scratch that educational itch I’d signed up for a course at Berkeley University as part of their summer program, Computational Models of Cognition. I figured that being in a university environment would be stimulating, I’d meet a load of like-minded people, the topic would give me an opportunity to look at biological aspects of intelligence (the day job focusing on silicon), and going a bit deeper on machine learning theory couldn’t hurt.

In practice my experiences were mixed. Where I’d expected to be one of many mature students along for the ride (Bay Area! Cognition! AI! 2022!), I seemed to be the only attendee over the age of 27. This was OK and everyone was very sweet, but I’d met That Guy during my brief undergraduate time at Reading, and been That Guy once already at Sussex. On the ML theory side of things, we didn’t go as deep as I’d hoped - building a simple feedforward network from scratch but not much more. The biological side was much more interesting, forcing me to revisit GCSE chemistry as we looked into exactly how synapses fire and impressing upon me the overwhelming complexity of the brain as we looked at key circuits in the hippocampus.

To pad this out, I took the excellent Brain Inspired Neuro AI course, an online effort from Paul Middlebrooks who runs a podcast of the same name. This course examined the same subjects, a little more broadly and superficially than the Berkeley course, and very capably. I particularly liked how Paul had extended the prerecorded lectures with regular calls for questions which he then answered in follow-up videos; and after subscribing to his Patreon, I’ve been enjoying the Discord-based community around the podcast.

Lots of real life happened during this time too: visits from my dad and an old friend from Brighton, both of which triggered some explorations of California countryside; a bout of COVID which passed through me and Kate, but (thanks perhaps to diligent masking and extreme ventilation) avoided our daughter B; we lost a much-loved cat; and B and I started learning to roller-skate in GGP. I also resurrected my Birdweather station - for reasons work-related and personal, ambient birdsong tracking has become interesting to me - and indulged an interest in bee navigation which I wrote about previously.

I read a lot. Here are some books I particularly enjoyed during this time; all are excellent and recommended.

• Don’t Point That Thing at Me, by Kyril Bonfiglioli - laugh-out-loud 70s cloak-and-dagger novel, starring an alcoholic middle-aged art historian.
• Lanny, by Max Porter - failing marriages, ancient spirits and the abduction of a child from an English village. Beautifully written from the author of the incredible Grief Is The Thing With Feathers.
• The self-assembling brain, Peter Robin Hiesinger - how do brains develop? Our models are static but biological systems grow, and the mechanism of their unfolding growth seem important to the end-results (perhaps but perhaps not essentially) and their efficient genetic coding (definitely).
• Seeing like a state, by James C Scott - the need for society to be legible to a state apparatus leads to an imposition of top-down order; the models needed are wrong, even if some are useful, and forcing your reality to conform to a model doesn’t work. Hard not to see the connections between the emancipatory nature of high modernism and modern tech culture - “we’re building better worlds”…
• Build, by Tony Fadell - on the topic of building software/hardware products, and excellent. I started finding this a bit trite, but as I worked through it I loved it more and more. Chapter 6 in particular was an astonishing record of what it’s like to actually sell to Big Tech.
• The Prince Of The Marshes, Rory Stewart, an account of the author’s time as an acting governor in post-war Iraq, with a theme of the importance of devolution throughout. I became a bit of a Rory Stewart fanboy after reading The Places In Between (on James’ recommendation) and have really been enjoying his podcast with Alastair Campbell, The Rest is Politics
• Head, hand, heart by David Goodhart, follow-up to the excellent Road To Somewhere, about the over-privileging of cognitive ability (relative to manual and caring skills) and how it’s damaged society.
• The Upswing, Robert Puttnam, a follow-up to Bowling Alone which seems to throw its predecessor under the bus in looking back further and plotting many aspects of American society on an inverted U-curve during the 20th century… with a common sentiment that while things are bad, but we’ve been here before and prevailed. Exhaustive, fascinating, ultimately optimistic.
• What is life, Addy Pross: how does chemistry become biology? A similar question to Gödel Escher Bach I guess, but lays out evolutionary principles: replication of simple molecules in a finite environment leads to competition and thus efficiency; then energy-harvesting arrives, and you have life.

(sorry)

I’ve been on a break from work for the last few months, and one of the things I’ve been doing is learning more about the brain: by taking Computational Models of Cognition as part of Berkeley University’s Summer Sessions, doing the (excellent) Brain Inspired Neuro-AI course, and of course listening and reading around the topic. I’ll write more about this another time, maybe.

I was charmed by this interview on the Brain Inspired podcast with Mandyam Srinivasan. His career has been spent researching cognition in bees, and his lab has uncovered a ton of interesting properties, in particular how bees use optical flow for navigation, odometry and more. They’ve also applied these principles to drone flight - you can see some examples of how here.

Some of the mechanisms they discovered are surprisingly simple; for instance, they noticed that when bees entered the lab through a gap (like a doorway), they tended to fly through the center of the gap. So they set up experiments where bees flew down striped tunnels, while they moved the stripes on one side, and established that the bess were tracking the speed of motion of their field of view through each eye, and trying to keep this constant. Bees use a similar trick when landing: keeping their speed, measured visually, at a constant rate throughout. As they get nearer to the landing surface, they naturally slow down. Their odometry also turns out to be visual.

The algorithm for centering flight through a space is really simple:

1. Convert what you see to a binary black-and-white image.
2. Spatially low-pass filter (i.e.blur) it, turning the abrupt edges in the image into ramps of constant slope.
3. Derive speed by measuring the rate of change at these ramps. If you just look at the edge of your image, you’ll see it pulses over time: the amplitude of these pulses is proportional to the rate of change of the image and thus its speed.
4. Ensure the speed is positive regardless of direction of movement.

Srinivasan did this using two cameras, I think (and his robots have two cameras pointing slightly obliquely). I tried using a single camera and looking at the edges.

It seems to work well on some test footage. Here’s a video I shot on a pathway in Sonoma, and here’s the resulting analysis which shows the shifts I was making between left and right during that walk, quite clearly:

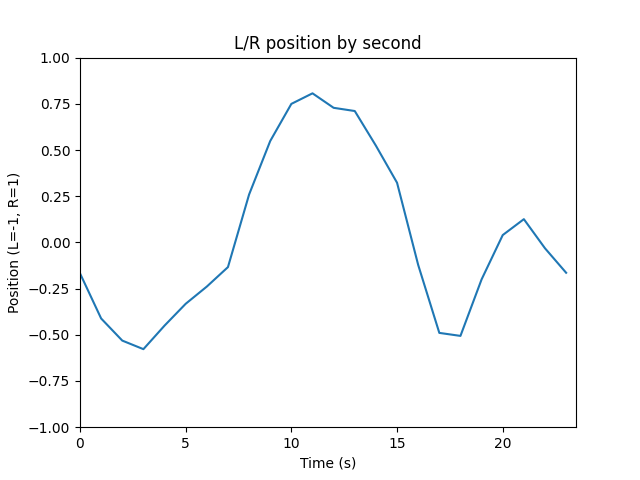
Things I’m wondering about now:

• Making it work for robots: specifically, can I apply this same mechanism to make a Donkey car follow a track? (I’ve tried briefly, no luck so far)
• Do humans use these kinds of methods, when they’re operating habitually and not consciously attending to their environment? Is this one of a bag of tricks that makes up our cognition?
• What’s actually happening in the bee brain? Having just spent a bit of time learning (superficially) about the structure of the human brain, I’m wondering how bees compare. Bees have just a million neurons versus our 86 billion. It should be easier to analyze something 1/86000 of the size of the human brain, no? (fx: c elegans giggling)

Srinivasan’s work is fascinating by the way: I loved how his lab has managed to do years of worthwhile animal experiments with little or no harm to the animals (because bees are tempted in from outside naturally, in exchange for sugar water, and are free to go).

They’ve observed surprisingly intelligent bee behavior: for instance, if a bee is doing a waggle-dance near a hive to indicate food at a certain location, and another bee has been to that location and experienced harm, the latter will attempt to frustrate the former’s waggle-dance by head-butting it. That seem very prosocial for an animal one might assume to be a bundle of simple hardwired reactions! After reading Peter Godfrey-Smith’s Metazoa earlier this year, has me rethinking where consciousness and suffering begin in the tree of life.

I’ve put the source code for my version here.

I found this dusty old box in a cupboard, dug out a few old cables and plugged it in. I wonder if it works?

What if neural networks, but not very good and lots of them?

I recently read A Thousand Brains, by Jeff Hawkins. I’ve been a fan of his since reading the deeply inspirational founding stories of the Palm Pilot (original team: 7 people! 7!). And as an AI weenie, when I discovered what he really wanted to do all along was understand intelligence, I was doubly impressed - and loved his first book, On Intelligence.

Paraphrasing one of the theses of A Thousand Brains: the neocortex is more-or-less uniform and composed of ~150k cortical columns of equivalent structure, wired into different parts of the sensorimotor system. Hawkins suggests that they all build models of the world based on their inputs - so models are duplicated throughout the neocortex - and effectively “vote” to agree on the state of the world. So, for instance, if I’m looking at a coffee cup whilst holding it in my hand, columns receiving visual input and touch input each separately vote “coffee cup”.

The notion of many agents coming to consensus is also prominent in Minsky’s Society of Mind, and in the Copycat architecture which suffuses much of Hofstadter’s work. (I spent a bit of time last year noodling with the latter).

We think the brain doesn’t do backprop (in the same way as neural networks do - Hinton suggests it might do something similar, and some folks from Sussex and Edinburgh have recently proposed how this might work). We do know the brain is massively parallel, and that it can learn quickly from small data sets.

This had me wondering how classical neural networks might behave, if deployed in large numbers (typically called “ensembles”) that vote after being trained weakly - as opposed to being trained all the way to accurate classification in a single network. Could enormous parallelism compensate in some way for either training time or dataset size?

Past work with ensembles

One thing my Master’s (pre-Google) gave me an appreciation for was digging into academic literature. I had a quick look around to see what’s been done previously - there’s no real technical innovation for this kind of exploration, so I expected to find it thoroughly examined. Here’s what I found.

Really large ensembles haven’t been deeply explored:

• Lincoln and Skrzypek trained an ensemble of 5 networks and observed better performance over a single network.
• Donini, Loreggia, Pini and Rossi did experiments with 10.
• Breiman got to 25 (“more than 25 bootstrap replicates is love’s labor lost”), as did Opitz and Maclin

Voting turns up in many places:

• Drucker et al point to many studies of neural networks in committee, initialized with different weights, and suggest an expectation I share: that multiple networks might converge differently and thus have performance improved in combination. They had explored this in previous work (Drucker et al 1993a).
• Donini, Loreggia, Pini and Rossi reach the same conclusion and articulate it thus: “different neural networks can generalize the learning functions in different ways as to learn different areas of the solutions space”. They also explore other voting schemes.
• Clemen notes that “simple combination methods often work reasonably well relative to more complex combinations”, generally in forecasting.
• Kittler, Duin and Matas similarly note that “the sum rules out performs other classifier combinations schemes”.

Breiman’s Bagging (short for “bootstrap aggregating”) seems very relevant. It involves sampling from the same distribution and training a different network on each sample, then combining their results via voting etc. Technically if you sampled fully from that distribution and thus trained all your ensemble of the same dataset, this would be bagging, but it seems a bit over-literal and incompatible in spirit.

In his paper Breiman does not explore the impact of parallelization on small dataset sizes, but does note that “bagging is almost a dream procedure for parallel computing”, given the lack of communication between predictors.

Finally, two other titbits stood out:

1. Perrone and Cooper observe that training on hold-out data is possible with an ensemble process without risking overfitting, as we “let the smoothing property of the ensemble process remove any overfitting or we can train each network with a different split of training and hold-out data”. That seems interesting from the POV of maximizing the value of a small dataset.
2. Krogh and Vedelsby have an interesting means to formalize a measure of ambiguity in an ensemble. Opitz and Maclin reference them as verifying that classifieds which disagree strongly perform better. I wondered if this means an ensemble mixing networks designed to optimize for individual class recognition might perform better than multiclass classifiers?

Questions to ask

All this left me wanting to answer a few questions:

1. What’s the trade-off between dataset size and ensemble size? i.e. would parallelization help a system compensate for having very few training examples, and/or very little training effort?
2. Is an ensemble designed to do multiclass classification best served by being formed of homogenous networks, or specialist individual classifiers optimized for each class?
3. How might we best optimize the performance of an ensemble?

I chose a classic toy problem, MNIST digit classification, and worked using the Apache MXNet framework. I chose the latter for a very poor reason: I started out wanting to use Clojure because I enjoy writing it, and MXNet seemed like the best option…. but I struggled to get it working and switched to Python. shrug

The MNIST dataset has 60,000 images and MXNet is bundled with a simple neural network for it: three fully connected layers with 128, 64 and 10 neurons each, which get 98% accuracy after training for 10 epochs (i.e. seeing 600,000 images total).

What’s the trade-off between dataset and ensemble size?

I started like this:

1. Taking a small slice of the MNIST data set (100-1000 images out of the 60,000), to approximate the small number of examples a human might see.
2. Training on this small dataset for a very small number of epochs (1 to 10), to reflect the fact that humans don’t seem to need machine-learning quantities of re-presented data.
3. Repeating the training for 10,000 distinct copies of a simple neural network.
4. For increasingly sized subsets of these 10,000 networks, having them vote on what they felt the most likely outcome was, and taking the most voted result as the classification. I tested on subsets to try and understand where the diminishing returns for parallelization might be: 10 networks? 100? 1000?

I ran everything serially, so the time to train and time to return a classification were extremely long: in a truly parallel system they’d likely be 1/10,000th.

I ran two sets of tests:

1. With dataset sizes of 200, 500, 1000 and 10000 examples from the MNIST set, all trained for a single epoch. I also ran a test with a completely untrained network that had seen no data at all, to act as a baseline.
2. For a dataset of 200 examples, I tried training for 1, 10, and 100 epochs.

It’s worth reiterating: these are very small training data sets (even 10,000 is 1/6th of the MNIST data set).

I expected to see increased performance from larger data sets, and from more training done on the same data set, but I had no intuition over how far I could go (I assumed a ceiling of 0.98, given this is where a well-trained version of the MXNet model got to).

I hoped to see increased performance from larger ensembles I had no intuition about how far this could go.

I expected the untrained model to remain at 0.1 accuracy no matter how large the ensemble, on the basis that it could not have learned anything about the data set, so its guesses would be effectively random.

Results

For dataset sizes trained for a single epoch (data):

Interpreting this:

• A larger dataset leads to improved accuracy, and faster arrival at peak accuracy: for d=10000 1 network scored 0.705, an ensemble of 50 scored 0.733 and by 300, the ensemble converged on 0.741 where it remained.
• For smaller datasets, parallelization continues to deliver benefits for some time: d=200 didn’t converge near 0.47 (its final accuracy being 0.477) until an ensemble of ~6500 networks.
• An untrained network still saw slight performance improvements (0.0088 with 1 network, to the 0.14 range by 6000.

Looking at the impact of training time (in number of epochs) (data):

Interpreting:

• More training means less value from an ensemble: 100 rose from 0.646 accuracy with 1 network to 0.667 by 50 networks, and stayed there.
• Less training means more value from an ensemble: 1 epoch rose from 0.091 accuracy to 0.55 by the time the ensemble reached 4500 networks.

Conclusions here:

1. Parallelization can indeed compensate for either a small dataset or less time training, but not fully: an ensemble trained on 10,000 examples scored 0.744 vs 0.477 for one trained on 200; one trained for 100 epochs scored 0.668 vs 0.477 for one trained for 1 epoch.
2. I don’t understand how an untrained network gets better. Is it reflecting some bias in the training/validation data, perhaps? i.e. learning that there are slightly more examples of the digit 1 than 7 etc?

Should individual classifiers be homogenous or heterogeneous?

Instead of training all networks in the ensemble on all classes, I moved to a model where each network was trained on a single class.

To distinguish a network’s target class from others, I experimented with different ratios of true:false training data in the training set (2:1, 1:1, 1:2, and 1:3)

I took the best performing ratio and tried it with ensembles of various sizes, trained for a single epoch on data sets of different sizes. I then compared these to the homogenous networks I’d been using previously.

And finally, I tried different data set sizes with well-trained ensembles, each network being trained for 100 epochs.

Results

Here’s a comparison of those data ratios (data):

I ended up choosing 1:2 - i.e. two random negative examples from different classes presented during training, for each positive one. I wanted to be in principle operating on “minimal amounts of data” and the difference between 1:2 and 1:3 seemed small.

Here’s how a one-class-per-network approach performed (each network trained for a single epoch, (data)):

And then, to answer the question, I compared 1-class-per-network to all-networks-all-classes (data):

Naively, a network trained to classify all classes performed better. But consider the dataset sizes: each all-classes network is trained on 10,000 examples (of all classes), but each per-class network of d=10000 is trained on 1/10 as much data. So a fair comparison is between the d=10000 per-class network and d=1000 all-class network, where per-class networks have the edge.

Here’s the result of well-trained ensembles (data):

This was a red flag for ensembles generally: repeated re-presentation of the same data across multiple epochs reached peak performance very fast. When the network was well trained, using an ensemble didn’t have any noticeable effect. Expanding on the far left of that graph, you can see that in the slowest case (20 examples per dataset) ensembles larger than 50 networks had little effect, but smaller ones did perform better:

How could we optimize the training of an ensemble?

A friend suggested I experiment with the learning rate for small datasets - reasoning that we want individual networks to converge as quickly as possible, even if imperfectly, and rely on voting to smooth out the differences. The default learning rate in MXNet was 0.02; I compared this to 0.1, 0.2, 0.3, and 0.4, all for networks shown few examples and given a single epoch of training.

Finally, I wondered how performance changed during training: imagine a scenario where each network is trained on a single extra example (+ negatives) and then the ensemble is tested. How does performance of the ensemble change as the number of examples grows? This might be a good approximation for an ensemble that learns very slowly and naturally in-the-wild, in line with the kinds of biological plausibility that originally interested me.

Results

A learning rate of 0.2 seemed to give the best results (data):

And here’s how that gradual learning worked out, as each ensemble size saw more examples (data):

An ensemble of 500 networks gets to ~0.75 accuracy by the time it’s seen 200 examples. Earlier results suggest it doesn’t go much further than that though.

Pulling it all together

Phew. This all took a surprising amount of time to actually run; I was doing it all on my Mac laptop, after finding that Colab instances would time out before the runs completed - some of them took a week to get through.

My conclusions from all this:

1. Large ensembles didn’t seem useful for getting to high accuracy classifications. Nothing I did got near to the 0.98 accuracy that this MXNet example could get to, well trained.
2. They did compensate for a dearth of training data and/or training time, to some degree. Getting to 0.75 accuracy with just 100 examples of each digit, just by doing it lots of times and voting, seemed… useful in theory. In practice I’m struggling to think of situations where it’d be easier to run 1000 ensembles than iterate over the training data a network has already seen.

In retrospect this might be explained as follows: a network is initialized with random weights, training it with a few examples would bias a set of these weights towards some features in the examples, but a slightly different set each time because of the randomness of the starting position. Thus across many networks you’d end up slightly biasing towards different aspects of the training data, and thus be able, in aggregate, to classify better.

Things I didn’t quite get to try:

1. Different voting schemes: I was super-naive throughout, and in particular wonder if I could derive some idea of confidence from different networks in an ensemble, just pick the confident ones?
2. MNist is a useful toy example, but I wonder if these results would replicate for other problems.
3. Applying the measure of ambiguity from Krogh and Vedelsby to my ensembles.

I finally got around to finishing GEB. I think I bought a copy 10-15 years ago and either gave up or got distracted during a couple of attempts to finish it; at my birthday last year I vowed to complete the thing, and I kept my promise a few months back.

Many of Hofstadter’s then-novel ideas (e.g. perception as the basis of cognition) seem more mainstream nowadays, but I got interested in some projects from his lab (FARG, the Fluid Analogies Research Group) around cognitively plausible architectures operating in microdomains.

A follow-up book, Fluid Concepts and Creative Analogies, goes into these in more detail, and I thought I’d have a go at reimplementing of one of their projects, initially for giggles but then to play with some of the underlying ideas a bit more.

Numbo is a simple number puzzle solver (UK readers: it’s the number puzzle from Countdown): given a set of 5 integers, apply mathematical operations to them to make a 6th target value. Classically a computer scientist might treat this as a search problem, but FARG was more interested in cognitive plausibility. You can find Daniel Defays’ original paper on Numbo here. I’m sure I’ve seen an OCR scan of the original source code at some point, but can’t find it now.

Numbo uses an architecture they called Copycat (from another project, called err Copycat, which investigated analogies like “abc is to pqr as bcd is to…?”). Numbo’s version of the Copycat architecture has 3 parts:

1. The Pnet, a network of static information: numbers, operations and basic calculations of a kind a child might learn by rote e.g. 2 + 2 = 4, 7 * 10 = 70.
2. The coderack, a store of priority-weighted processes (called codelets) which is sampled from probabilistically, and thus run in a slightly random order, effectively emulating parallelism even when run serially. Codelets operate on the cytoplasm and can create other codelets. They are independent processes and do not communicate with one another directly.
3. The cytoplasm, a working memory which is operated on by codelets sampled from the coderack, and stores current theories and constituent numbers.

My implementation is written in Clojure, partly because the original was Common Lisp but more because I enjoy writing Clojure. You can find it here; it can be run from the command-line, or there’s a GUI to help visualize a single run, plus a script which tries to solve each of 10 puzzles 100 times, which I’m using to track the effectiveness of changes I make. Because there’s a lot of random processes underlying Numbo, different runs can and do produce different results - or sometimes no results.

I’ve /just/ managed to get Numbo to a point where it solves 7/10 of the original sample puzzles, which in the spirit of “launching early enough to be embarrassed by my first version” seems like the right time for a push to GitHub. I have some ideas about the remaining 3 and other improvements - I suspect that speedy puzzle-solving is influenced by some of the decisions around decay rates of nodes in the Pnet and cytoplasm. There are a few other jumping-off points for future work:

• The contents of the Pnet are important; I’m interested in working out how you might construct a viable Pnet from e.g. educational materials;
• I wonder how codelets might be evolved rather than hand-coded;
• I wonder how transferable the architecture might be to a new micro domain.

Lots to think about! The process of writing this was also quite fun. It’s the largest program I’ve written since my Master’s dissertation on superoptimization (code, dissertation, paper). A few observations:

• I wrote the cytoplasm 3 times: the first one was too simple, the second too complex (but I got to learn about Clojure zippers) and the third one OK so far - but I think I’ve just found a bug which points to a error in my data model (around how secondary targets are treated)
• Writing a GUI to examine the state of runs was a good move: it’s saved me so a ton of time in debugging, as I can visually run through the evolving state of the cytoplasm, identify odd points by eye and dive in to debug them. Swing is still a PITA, even with Seesaw wrapping it.
• After starting to read Paul Graham’s On Lisp, I regret not having pulled key abstractions beyond library functions into macros. My codelets contain a ton of boilerplate and whilst I pulled out some functions to handle probabilistic sampling, I feel like this could be made into a part of the language a bit more.
• In a lovely demonstration of Conway’s Law, the needs of real life meant I had to write Numbo in tiny non-cooperating chunks which made individual sense. I left messages to future-me on what to do next but otherwise frequently lost state when I returned to work on it. Given all this, I became a set of tiny discrete processes acting towards a greater goal…